Fractals and other mathematical gimmicks
Through my father I came into contact with fractals at a very early age. The Motorola 68000 processor of the Atari ST was incredibly slow compared to today's computers, but compared to a manual calculation it was incredibly fast. And so my first attempts at designing algorithms were in the area of fractals. Probably already in my school days it became clear that the connection of computers and aesthetics is close to my heart.
The classical fractal, the Mandelbrot set, as well as the Julia set are only suitable for the representation on 2D plotters. However, in the area of two-dimensional fractals, such as the Koch, Hilbert or Gosper curve, one can find very exciting templates. Fractals that can be described as space-filling curves are excellent, especially if you add a little vector magic from Illustrator. This can be distortions, but also the doubling of lines or the rounding of corners.
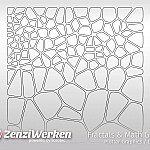
Also coming from the field of mathematics are the Voronoi structures, which I have already used in my trivets. Even though the Ukrainian mathematician is not the first discoverer of these diagrams, the term has gained acceptance over Dirichlet decomposition. It is interesting to note that these diagrams also occur in nature. While geology, meteorology, and still crystallography may be related subjects, it is surprising that the structures also occur in ecology, anatomy, and physics in general.
Another pattern is the Turing pattern. It arises from the interaction of various chemical reactions in a fluid environment and was introduced in 1950 by the English mathematician Alan Turing. The pattern is often used as an example of self-organization in natural processes. Since this 'Reaction Diffusion' can also be used to convert gray levels, one gets into the embarrassment of mapping surfaces. I have solved this problem by creating concentric lines.
And of course there are other mathematical ideas that can be nicely implemented as two-dimensional graphics. Repeated crossing lines can form nice moiree patterns. And curve graphs also elicit wonderful images from mathematics.
The following pages will help you create the above graphics: